Geometria Espacial: Conceitos, Fórmulas, Sólidos Geométricos e Exercícios Resolvidos

 

A Geometria Espacial é o ramo da Matemática que estuda as formas geométricas no espaço, ou seja, aquelas que possuem três dimensões: comprimento, largura e altura. Esse conteúdo é amplamente cobrado no ensino fundamental, médio, ENEM e em provas de concursos públicos, além de ter inúmeras aplicações práticas no dia a dia.

Neste artigo completo, você vai aprender:

• O que é Geometria Espacial
• Diferença entre Geometria Plana e Espacial
• Principais sólidos geométricos
• Fórmulas de área e volume
• Conceitos fundamentais
• Exemplos explicados
• Exercícios com gabarito

---

O que é Geometria Espacial?

A Geometria Espacial estuda os objetos geométricos que ocupam lugar no espaço e apresentam volume. Diferentemente das figuras planas, como quadrados e círculos, as figuras espaciais são tridimensionais.

📌 Exemplos de objetos estudados pela Geometria Espacial:

• Cubo
• Paralelepípedo
• Pirâmide
• Prisma
• Cilindro
• Cone
• Esfera

Esses sólidos aparecem em construções, embalagens, objetos do cotidiano e projetos de engenharia.

---

sólidos geométricos em 3D

---

Diferença entre Geometria Plana e Geometria Espacial

A compreensão dessa diferença é essencial para não confundir fórmulas e conceitos.

Geometria Plana	Geometria Espacial
Estuda figuras bidimensionais	Estuda figuras tridimensionais
Possui área e perímetro	Possui área total e volume
Não ocupa espaço	Ocupa espaço

👉 Enquanto a Geometria Plana trabalha com superfícies, a Geometria Espacial analisa corpos geométricos.

Leia Mais: Área e Perímetro: Conceitos, Fórmulas e Exercícios Resolvidos

---

Conceitos Fundamentais da Geometria Espacial

Antes de estudar os sólidos, é importante compreender alguns conceitos básicos.

Ponto

É uma posição no espaço, não possui dimensão.

Reta

Conjunto infinito de pontos alinhados.

Plano

Superfície plana e infinita, sem espessura.

Aresta

Segmento de reta que liga dois vértices de um sólido.

Vértice

Ponto de encontro das arestas.

Face

Superfície plana que limita um sólido geométrico.

---

Poliedros e Corpos Redondos

Os sólidos geométricos são classificados em dois grandes grupos.

Poliedros

São sólidos formados apenas por faces planas.

Exemplos:

• Cubo
• Paralelepípedo
• Prismas
• Pirâmides

Corpos Redondos

Possuem superfícies curvas.

Exemplos:

• Cilindro
• Cone
• Esfera

---

comparação entre poliedros e corpos redondos

---

Prismas

Os prismas recebem nomes conforme o polígono de suas bases.

O prisma é um poliedro que possui:

• Duas bases paralelas e congruentes
• Faces laterais retangulares

Tipos de prismas

• Prisma triangular
• Prisma quadrangular
• Prisma pentagonal

Fórmulas do prisma

• Volume do prisma

O volume de todo prisma é a multiplicação entre a medida de sua área da base pela sua altura (h).

A altura h do prisma é a distância entre suas bases.

• Área do prisma

O cálculo da área da base depende do polígono que forma suas bases. Já a área lateral é a soma das áreas dos retângulos que formam sua lateral.

---

Exemplo de prisma

Um prisma de base quadrada com lado 4 cm e altura 10 cm:

Área da base = 4 × 4 = 16 cm²

• Volume = 16 × 10 = 160 cm³

---

Pirâmides

A pirâmide é um poliedro que possui:

• Uma base poligonal
• Faces laterais triangulares
• Um vértice no topo

Tipos de pirâmides

• Pirâmide triangular
• Pirâmide quadrangular
• Pirâmide pentagonal

Fórmulas da pirâmide

De forma geral, o volume da pirâmide é calculado pela multiplicação entre a área da base e sua altura, dividindo o resultado por 3.

Volume:

• V = (área da base × altura) ÷ 3

Área da pirâmide

A medida da área da pirâmide é a soma da área de sua base mais sua lateral.

---

As pirâmides recebem nomes conforme o polígono de suas bases.

---

Exemplo de pirâmide

Uma pirâmide de base quadrada com área da base igual a 36 cm² e altura 9 cm:

V = (36 × 9) ÷ 3 = 108 cm³

---

Cubo

O cubo é um caso especial de prisma, no qual:

• Todas as faces são quadradas
• Todas as arestas possuem a mesma medida

O cubo é um hexaedro regular composto de 6 faces quadradas, 12 arestas e 8 vértices.

Fórmulas do cubo

Área total:

• A = 6 × aresta² (6 x a²)

Área lateral do cubo

Volume:

• V = aresta³ (a³)

---

Exemplo de cubo

Um cubo com aresta de 5 cm:

• Área total = 6 × 25 = 150 cm²
• Volume = 5³ = 125 cm³

---

Paralelepípedo

O paralelepípedo retângulo é um sólido com faces retangulares.

O paralelepípedo é formado por 6 faces retangulares, 12 arestas e 8 vértices. Diferente do cubo, as medidas das arestas do comprimento, da largura e da altura, não possuem necessariamente a mesma medida.

Sendo: L a medida da largura, c do comprimento e a da altura.

Fórmulas do paralelepípedo

Volume do paralelepípedo

Área total do paralelepípedo

Onde:

• c = comprimento
• L = largura
• a = altura

---

---

Cilindro

O cilindro é uma forma espacial arredondada, por isso, não é considerado um poliedro. É formado por duas bases circulares e paralelas. A distância entre suas bases é sua altura.

O cilindro é um corpo redondo que possui:

• Duas bases circulares
• Uma superfície lateral curva

Fórmulas do cilindro

A área total é formada pela soma das áreas das duas bases com sua área lateral.

Onde:

---

Exemplo de cilindro

Um cilindro com raio 3 cm e altura 10 cm:

V = 3,14 × 3² × 10 = 282,6 cm³

---

Cone

Sendo, r o raio da base e h a altura e g a geratriz.

O cone possui:

• Uma base circular
• Um vértice no topo
• Superfície lateral curva

Fórmulas do cone

Volume do cone

Área da lateral do cone

Área da base do cone

---

---

Esfera

A esfera é o sólido geométrico totalmente arredondado.

Fórmulas da esfera

Volume da esfera

Área da esfera

---

Exemplo de esfera

Uma esfera com raio de 6 cm:

V = (4 × 3,14 × 6³) ÷ 3 = 904,32 cm³

Sólidos de Platão

Os sólidos platônicos são poliedros especias, eles são formados por faces iguais. Todas as faces destes sólidos são polígonos regulares.

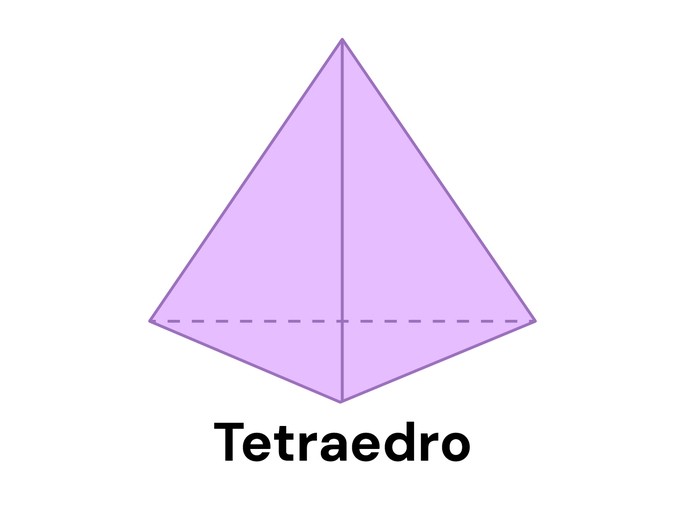
Tetraedro

O Tetraedro é um poliedro regular composto de 4 faces triangulares, 6 arestas e 4 vértices.

Volume do tetraedro

Área total do tetraedro

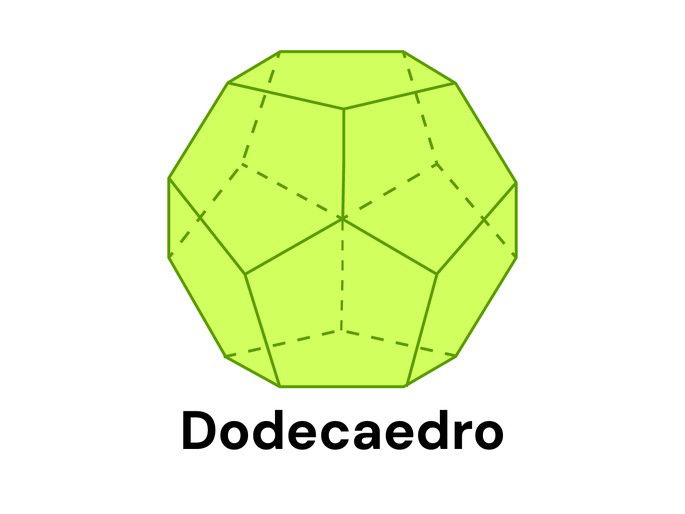
Dodecaedro

O Dodecaedro é um poliedro regular composto de 12 faces pentagonais regulares, 30 arestas e 20 vértices.

Remover anúncios

Volume do dodecaedro

Aproximadamente, o volume do dodecaedro é:

Área total do dodecaedro

Aproximadamente, a área do dodecaedro é:

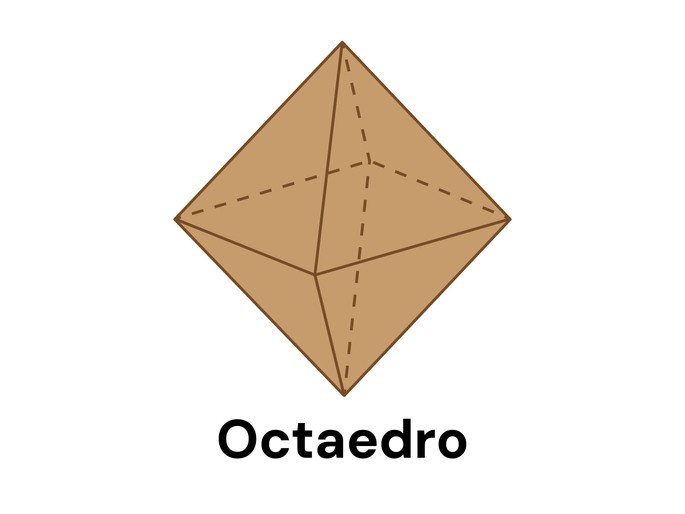
Octaedro

O Octaedro é um poliedro regular de 8 faces triangulares, sendo todas triângulos equiláteros. Ele possui 12 arestas congruentes e 6 vértices.

Volume do octaedro

Aproximadamente, o volume do octaedro é:

Área do octaedro

Aproximadamente, a área do octaedro é:

Icosaedro

O Icosaedro é um poliedro convexo composto de 20 faces triangulares, 30 arestas e 12 vértices.

Volume do Icosaedro

Aproximadamente, o volume do icosaedro é:

Área do Icosaedro

Aproximadamente, a área do octaedro é:

---

Aplicações da Geometria Espacial no Dia a Dia

A Geometria Espacial está presente em diversas áreas:

• Arquitetura
• Engenharia
• Design
• Construção civil
• Embalagens

• Indústria

Calcular volumes e áreas ajuda a estimar custos, materiais e espaços.

---

Exercícios de Geometria Espacial

1️⃣ Calcule o volume de um cubo com aresta 4 cm.

2️⃣ Um cilindro possui raio 5 cm e altura 8 cm. Qual é o volume?

3️⃣ Uma pirâmide tem área da base de 20 cm² e altura de 9 cm. Determine o volume.

Gabarito

1️⃣ V = 4³ = 64 cm³
2️⃣ V = 3,14 × 25 × 8 = 628 cm³
3️⃣ V = (20 × 9) ÷ 3 = 60 cm³

Exercícios sobre geometria espacial

Exercício Extra

Um aquário é aberto na parte de cima, com formato de paralelepípedo reto retangular e 60 cm de comprimento, 40 cm de largura e 30 cm de altura. Qual é a sua área total e seu volume, respectivamente?

a) 8400 cm² e 72000 cm³

b) 7200 cm² e 72000 cm³

c) 7200 cm² e 36000 cm³

d) 4800 cm² e 24000 cm³

e) 3200 cm² e 24000 cm³

---

Gabarito explicado

Dados do problema:

• Comprimento (c): 60 cm
• Largura (l): 40 cm
• Altura (h): 30 cm

Cálculo da área total:

Como mencionamos anteriormente, a área total de um paralelepípedo é a soma das áreas de suas faces. No caso do aquário, consideremos apenas as cinco faces (desconsiderando a parte superior, que está aberta).

1. Identificar as faces:

• Frente e trás: São dois retângulos iguais com as dimensões comprimento e altura.
• Lados: São dois retângulos iguais com as dimensões largura e altura.
• Fundo: Um retângulo com as dimensões comprimento e largura.

2. Calcular a área de cada tipo de face:

Área da frente e de trás: 2 × (comprimento × altura) = 2 × (60 cm × 30 cm) = 3600 cm²

Área dos lados: 2 × (largura × altura) = 2 × (40 cm × 30 cm) = 2400 cm²

Área do fundo: comprimento × largura = 60 cm × 40 cm = 2400 cm²

3. Somar as áreas de todas as faces:

Área total = 3600 cm² + 2400 cm² + 2400 cm² = 8400 cm²

Portanto, a área total da superfície do aquário é de 8400 centímetros quadrados.

Cálculo do volume:

Fórmula para calcular o volume de um paralelepípedo:

Volume = comprimento × largura × altura

V = c × l × h

Substituindo os valores:

V = 60 cm × 40 cm × 30 cm

V = 72.000 cm³

Portanto, o volume do aquário é de 72000 centímetros cúbicos.

Conclusão:

O aquário possui uma área de 8400 cm² e volume de 72000 cm³.

---

Conclusão

A Geometria Espacial é um dos conteúdos mais importantes da Matemática, pois permite compreender e calcular formas tridimensionais presentes no mundo real. Dominar seus conceitos e fórmulas é essencial para o sucesso escolar, acadêmico e em concursos públicos.

📘 Estudar com exemplos práticos e exercícios é a melhor forma de fixar o aprendizado.

---

• geometria espacial
• sólidos geométricos
• volume dos sólidos
• fórmulas de geometria espacial
• prismas e pirâmides

• corpos redondos